Tetraconeter

10VII2008-16VIII

quebecium.html

 

Systme du Qubcium.

Un ttracne pavant et son usage dans un tableau 3D des lments chimiques.

Pierre Demers

Sommaire. Quatre cnes ayant mme ouverture et mme sommet saturent exactement l'espace des angles solides si leur ouverture vaut 109,471o. Si de plus ils ont tous mme gnratrice, ayant tous une base circulaire semblable, ils forment une figure compose de surfaces cniques et de portions de plans. Je l'appelle ttracne, elle est compose de 4 volumes cniques. Le ttracne s'inscrit dans un ttradre rgulier et aussi dans un octadre que j'ai tudi prcdemment, identique au ttradre tronqu d'Archimde. Le ttracne participe aux proprits de pavage que j'ai dcrites pour cet octadre, permettant entre autres de raliser un tableau 3D des lments chimiques, un lment tant figur par un cercle et un volume conique, chaque ttracne figurant une ttrade d'lments. Je propose "pavage" faute d'un meilleur terme, puisque l'occupation de l'espace est incomplte. La prsente sorte de pavage laisse inoccups des espaces l'intrieur et l'extrieur des ttracnes. Quatre est un nombre privilgi dans ce qui prcde puisqu'il est associ aux ttrades d'lments, chaque lment chimique appartenant une ttrade. - Le ttracne peut tre reprsent soit par les seules 4 surfaces gauches, soit par les seules 4 surfaces planes. Il s'en suit 2 types, A et B, de tableaux 3D des lments chimiques. - J'examine la possibilit qu'il existe des figures comparables au ttracne mais formes de n cnes avec n diffrent de 4. Je montre que cette possibilit existe pour n = 6  ou 12, il existe l'hexacne et le dodcacne, pourvus eux aussi de la proprit de pavage indfini. On ne peut pas dire que chaque lment chimique appartient une hexade ou une dodcade.

 

Introduction.

Le prsent travail continue un autre travail de 2008, lequel  continuait celui de 2005, dont les figures 3 et 4 montrent des patrons triangulaires de ttradres, composs d'un triangle central entour de 3 triangles extrieurs. 967 http://www.lisulf.quebec/Atomesentetradeshtml

Le travail de 2008 est  intitul Un octadre pavant etc. 1001 http://www.er.uqam.ca/nobel/c3410/Unoctaedrebis.htm

 

Ces rsultats dcoulent de l'tude que je poursuis depuis 2004 de la gomtrie des cnes de prcession du moment cintique propre de l'lectron ou spin, dont l'ouverture est fixe par la thorie la valeur de 109,471o. Quatre de ses cnes forment une association naturelle pour dfinir un ttradre rgulier. J'ai suggr qu'il y a l une explication de la symtrie d'ensemble d'ordre 4 du tableau des lments chimiques, une raison de grouper ces lments en ttrades, j'ai par suite prsent un tableau 2D des lments en ttrades, lequel prend l'aspect d'un quart d'ellipse. Dans un tel tableau, les ttrades sont figures par une grande case carre divise en 4 petites cases carres. J'ai montr que l'octadre pavant mentionn ci-dessus permet de raliser un tableau 3D de 30 octadres. Voyez la figure 15 http://www.er.uqam.ca/nobel/c3410/Unoctaedrebis.htm. J'ai maintenant aperu une proprit remarquable appartenant au groupement de 4 des cnes de prcession : il s'incrit dans un octadre pavant et participe par suite de ses proprits de pavage. Ce groupement, je l'appelle ttracne.

 

La gnratrice du cne mesurant 5 cm, sa base est un cercle de rayon 4,0825 cm, qui s'inscrit dans un triangle de ct 14,14 cm et dans un hexagone de ct 4,71 cm. Le ttradre circonscrit a une arte de 14,14 cm, l'octadre circonscrit a une arte de 4,71 cm. Voyez Fig. 1, http://www.lisulf.quebec/GQ1sur2

 

Expos.

La possibilit apparat donc de raliser un tableau 3D des lments constitu de 30 ttracnes, chacun tant inscrit dans l'un des octadres du tableau de 30 octadres de la figure 15 mentionne ( http://www.er.uqam.ca/nobel/c3410/Unoctaedrebis.htm).

 

Les ttracnes s'associent jointivement par le contact de leurs faces circulaires planes mais avec des vides. Je propose "pavage" faute d'un meilleur terme, puisque l'occupation de l'espace est incomplte. La prsente sorte de pavage laisse inoccups des espaces l'intrieur et l'extrieur des ttracnes. Si on compare la prsente figure un empilement de boulets de canons, elle ressemble plus un pavage proprement dit qu' cet empilement, o le contact entre boulets est ponctuel. - On peut voir dans cette possibilit une confirmation supplmentaire de la pertinence de faire intervenir la gomtrie pour expliquer le tableau des lments et la structure des atomes. Cette gomtrie tant celle des cnes de prcession du spin de l'lectron.

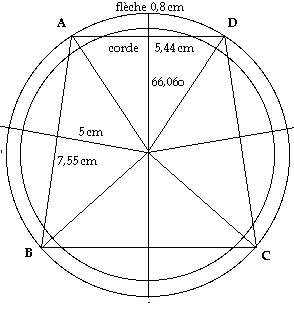
Fig. 1. Patron d'un cne dans la convention A. On dcoupe en laissant une patte le long de OD et on applique OA sur OD.  La patte sert raccorder par collage les lignes OA et OD, O centre. PatronCone.gif, TCfig1.gif

Voyez le patron d'un cne Fig. 9. Ttradre rgulier associ aux spins 0,5/0,5 et 3/2 Patron sur une feuille plane servant obtenir un cne d'ouverture 109,471o du spin 0,5. Rayon 5 cm.Quatre de ces cnes gnrent un ttradre rgulier. D'aprs extrait de 970 en 2005 http://www.lisulf.quebec/GQ2sur2.html

 

Voici le patron d'un cne, fig.1. Le patron d'un tenant d'un ttracne dans la convention A, savoir sans les surfaces planes circulaires, fig. 2.

 

Fig. 2. Patron d'un ttracne d'un tenant..ConetetraRJVBquater.gif

On peut naturellent fabriquer 4 cnes sparment et les assembler ensuite, mais le prsent patron remplace certaines oprations d'assemblage par de simples pliages.

 

Fig. 3. Un ttracne inscrit dans 3 parois d'un octadre. TetrainscritOcta.gif

Un ttracne qui est incrit dans 3 parois d'un octadre, fig. 3.

Fig. 4. pavage de ttracnes. Exemple de 4 ttracnes. Faces R sur R, J sur V,

B sur V.Tetras4.gif

Un pavage restreint de ttracnes : 4 ttracnes , faces R sur R, J sur V, V sur V, fig. 4.

Fig. 5. nantiomorphes. RJVetRJB.gif

Si on discerne les cnes constituants d'un ttracne, par exemple par les couleurs RJVB, 2 nantiomorphes se manifestent. RJVB et RJBV ne se superposent pas, fig. 5. Le ttracne est un objet chiral.

Fig. 6. Les 4 strates formes de 30 ttracnes. Tesstra1234.gif

Voici un tableau 3D des 4 strates formes de 30 ttracnes, fig. 6.

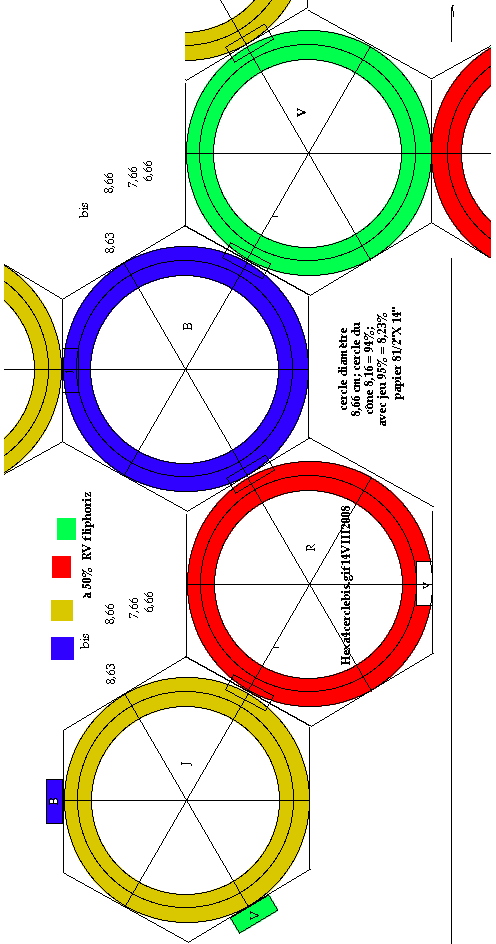
Fig. 7. Patron d'un tenant d'un ttracne, convention B. TCfig7.gif

Dans la convention B maintenant, voici le patron d'un tenant d'un ttracne, fig. 7. Chaque cercle du ttracne est entour d'un hexagone circonxcrit.

 

Convention B. Tableau 3D.

Les strates peuvent maintenant se figurer par des agencements de ttracnes. Figure 8 gauche, la face circulaire plane des cnes n'est pas figure, c'est la convention A. droite, au contraire, la face circulaire est seule figure, c'est la convention B.

Fig. 8.  Un ttracne convention A, convention B. Dans la convention B, faites oeuvre d'imagination. Imaginez le point central, de ce point, imaginez pour chaque face une droite gnratrice s'appuyant sur la circonfrence extrieure de l'anneau color, et vous avez devant vous 4 cnes et un ttracne complet. Conecercle.gif

A La face circulaire plane des ttracnes est suggre et imagine. Figure 8 gauche, la face circulaire plane des cnes n'est pas figure.

 

B Figure 8 droite, au contraire, la face circulaire est seule figure, la surface de rvolution est suggre en imaginant le point central et la gnratrice en rvolution. Ces dernires figures ressemblent beaucoup la figure 15 mentionne ( http://www.er.uqam.ca/nobel/c3410/Unoctaedrebis.htm), sauf qu'on y considre des cercles au lieu  des hexagones qui les entourent.

Fig. 9. Strate 2 en ttracnes dans la convention B. TCfig9.gif

La strate 2 estreprsente 3D en ttracnes, fig. 9.

 

Autres multicnes pavants.

Six cnes ayant mme ouverture et mme sommet saturent exactement l'espace des angles solides si leur ouverture vaut 90o. L'hexacne ralis s'inscrit dans un cube. Avec 20 tels hexacnes, on dispose de 120 cnes ou de 120 carrs o inscrire le nom de chaque lment chimique, et on peut donc raliser une sorte de tableau 3D par pavage, ayant 5 tages de 4 cubes chacun, 24 lments par tage. Cette figure n'a pas de sens physique particulier. Fig 10.

Fig. 10. Tableau de 120 lments en 20 hexacnes  ou 20 cubes dans la convention B. Hexacone20bis.gif

Douze cnes ayant mme ouverture et mme sommet saturent exactement l'espace des angles solides si leur ouverture vaut 60o. Le dodcacne ralis s'inscrit dans un rhombododcadre pavant. Avec 10 tels dodcacnes, on dispose de 120 cnes ou de 120 losanges o inscrire le nom de chaque lment chimique, et on peut donc raliser une sorte de tableau 3D par pavage. Cette figure n'a pas de sens physique particulier.

Trac d'un multicne par le mouvement d'un point. Multicnes et pyramides.

Partant du sommet d'un cne, le point figuratif dcrit une gnratrice dans un mouvement centrifuge, puis une circonfrence dans une ligne ferme en entranant la gnratrice; il parcourt ensuite la gnratrice dans un mouvement centripte et revient au sommet du cne. Fig. 11.

Fig. 11. Mange d'un point figuratif. Le sens de rotation est droit pour un observateur plac au dessus de la base. TCfig11.gif

Puisque le sommet est commun tous les cnes, le point figuratif peut, sans qu'on ait lever la plume, reprendre le mme mange pour un 2e cne au choix et un 3e etc tant qu'il en est. De prfrence, on choisira le sens de rotation droit tel que vu de l'extrieur du cne.

 

Tous les cnes composant un multicne se prtent ce mode de trac par un mouvement ininterrompu d'un point figuratif, ceux pavants avec n = 4, 6, 12, ceux  non pavants issus des polydres rguliers avec n = 8, 12 et 20, et d'autres encore.

 

En remplaant la base circulaire par un polygone, une pyramide ayant ce polygone pour base se prte un tel mode de trac.

-30-

Tetraconeter

10VII2008-16VIII

quebecium.html