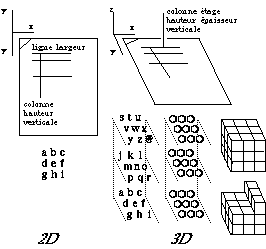
Figure 2.42. Matrices bi- et tri-dimensionnelles 3X3, 3X3X3. Empilement. Vocabulaire. Objets lettres, boules, cubes.
Pour
faire passer la
configuration du
Québécium d'une
représentation
unidimensionnelle à
la représentation
bidimensionnelle qui
précède, il nous a
fallu des démarches
peu
évidentes à première vue.
En
revanche, un moyen
de passer de deux à
trois dimensions
apparaît
immédiatement. Il
suffit de superposer
les strates. Nous
verrons dans la
suite d'autres
moyens plus
élaborés. Mais il
nous faut commencer
par un rappel sur
les matrices
tridimensonnelles.
Les matrices tridimensionnelles se décrivent en ajoutant des étages aux matrices bidimensionnelles en lignes et en colonnes. Elles sont des ensembles d'objets ordonnés en lignes, colonnes et étages, emplissant un espace parallélépipédique. Au lieu d'une feuille de papier qu'on a quadrillée, il nous faut plutôt imaginer un étagement d'espaces cubiques, les inférieurs supportant les supérieurs. L'analogue d'un tableau sera appelé un empilement. On peut généraliser à trois dimensions non trirectangles. Ces matrices envisagées dans toute leur généralité deviennent les réseaux des systèmes cristallins. Figure 2.42.

Figure 2.42. Matrices bi- et tri-dimensionnelles 3X3, 3X3X3. Empilement. Vocabulaire. Objets lettres, boules, cubes.
Notons
le double emploi des
mots hauteur, colonne et
verticale. Pour
éviter l'ambigu&itrem;té :
x et y sont dans le
plan de la feuille
de papier, z s'en
échappe.
La figure 2.21 n'a qu'un étage. Par des translations sans rotation et par des changements d'étage, nous amenons les strates l'une au dessus de l'autre. Dans le présent paragraphe, nous choisissons de placer les couronnes de mêmes couleurs et de mêmes désignations littérales l'une au dessus de l'autre. Les cases R sont alignées verticalement, de même les cases J et V. Nous allons obtenir des figures de symétrie quaternaire par rapport à l'axe des z. Dans un premier temps, nous traitons les 2 cases vides de la strate 1 comme si elles étaient pleines. Figure 2.43.
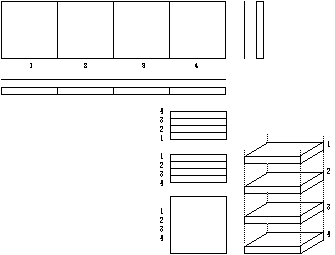
Figure 2.43.
Configuration
électronique du
Québécium. Passage
d'une représentation
bidimensionnelle à
une représentation
tridimensionnelle
(superposition).
Schématique. Vue
finale éclatée.
Strates types.
On a employé des strates types et on a obtenu une superposition matrice tridimensionnelle de 8 colonnes, 8 lignes et 4 étages, ayant 256 cases cubiques.
Dans
la figure suivante, on a
employé des strates
réduites et on a
obtenu un
empilement qui
s'inscrit dans la
matrice précédente.
On a le choix de
placer la strate 4
qui est la plus
vaste à la base ou
au sommet de la
superposition.
Placée à la base,
elle donne à l'empilement l'aspect d'une pyramide à base carrée, qui se concrétise aisément avec
des cubes de bois ou
d'autres matières. Figure 2.44.
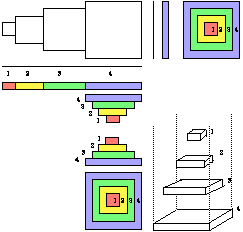
Figure 2.44. Configuration électronique du Québécium. Passage d'une représentation bidimensionnelle à une représentation tridimensionnelle, un empilement régulier. Schématique. Strates réduites. Pyramide à base carrée.
La figure suivante montre la pyramide à base carrée à une échelle plus grande. Les présentes figures montrent la configuration électronique du Québécium de façon schématique et plus ou moins abrégée. Figure 2.45.
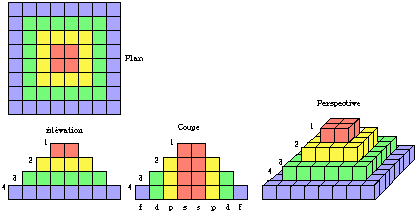
Figure 2.45. Empilement régulier des 4 strates. Pyramide à base carrée.
Ces
structures, idéales
ou concrètes, se
prêtent à la
création de
sous-ensembles,
eux aussi
empilements. Par exemple, ayant reconnu le présence des
couronnes, qui sont
au nombre de 10. on peut les assembler en quatre sous-ensembles qui sont des empilements distincts selon les catégories s, p, d et
f.
On obtient l'aspect
de cheminées emboîtées ou télescopées. On peut les dégager par des glissements verticaux. Il y a
4 cheminées : R, J,
V, B. La cheminée R
n'est pas creuse, la
cheminée B est peu
haute. Ces cheminées peuvent se télescoper pour redonner la pyramide originale, leur création à partir de cette pyramide est l'opposé d'un télescopage. Figure 2.46.

Figure 2.46. Quatre cheminées, quatre couleurs, quatre quanta azimutaux. 120 cases cubiques.
Ces cheminées étant produites, nous pouvons les assembler l'une au contact de l'autre sans télescopage. Dans l'espace creux qui subsiste, nous pouvons imaginer des cubes vides. Il en faut 80. La structure obtenue est un empilement de 200 cubes dont 118 occupés, haut de 10 étages. Figure 2.47.
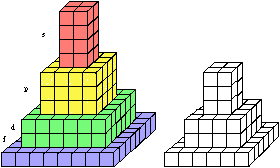
Figure 2.47. Les quatre cheminées superposées. Empilement de 120 cubes et de 80 autres cubes intérieurs vides, total 200. Les 80 cubes intérieurs.
Visibilité. Les représentations 3D d'un ensemble continu d'objets opaques posent invariablement des problèmes de visibilité, qu'elles soient dessinées ou concrétisées. C'est notoirement le cas des globes terrestres. Règle générale, on n'aperçoit d'un coup d'oeil que la moitié des données superficielles. Notons que la représentation en cheminées superposées laisse voir d'un coup d'oeil latéral 60 cubes sur 120, ce qui est un progrès sur la pyramide de la figure 2.45 qui, comparativement, laisse voir tout au plus 40 de ses 120 cubes. Cette pyramide en montre 64 en vue plongeante et elle en contient 20 qui restent cachés. En comparaison, les représentations 2D précédentes montrent la totalité des cases d'un coup d'oeil.
L'inspection de la pyramide figure 2.45 nous invite à faire glisser les strates l'une sur l'autre, par exemple d'une grandeur linéaire k selon l'axe des x, k étant mesurée en unités égales à l'arête des cases cubiques. Figure 2.48.
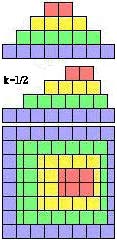
Figure 2.48. Glissement mutuel des strates. Profil, élévation, plan pour k = 1/2.
Une manière élégante de décrire ces glissements est de transformer les cases cubiques en prismes hexaèdriques à bases carrées où sont préservés le volume et la hauteur, ayant deux faces rectangulaires et deux faces parallélogrammes dépourvus d'angles droits. Ces prismes sont penchés, l'angle entre les nouveaux axes z et x étant phi au lieu de 90o, avec phi = arcctgk. L'identification des cases se fait sur leur face supérieure. Figure 2.49.
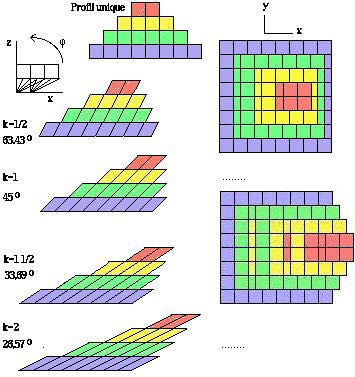
Figure 2.49. Coordonnées non trirectangles R2O1. Profil, élévations, plans pour diverses valeurs de k. En plan, on montre la face supérieure des prismes.
Ce faisant, nous passons du système de coordonnées trirectangle, en abrégé R3 à un système R2O1 où l'un des angles entre les axes est oblique. Pour spécifier un tel système, il faut énoncer entre quels axes l'angle est oblique et donner une mesure de cet angle, par une expression telle que celle q ui suit.
R2O[zx(phi, k)]
L'un des paramètres phi ou k suffit.
Le glissement des strates peut se faire dans le plan des xy et autrement que selon les axes x ou y, par exemple selon la diagonale principale entre ces axes. L'unité du déplacement sera la diagonale traversant une face des cases cubiques, résultante de deux déplacements égaux aux arêtes de ce cube à angle droit. Figure 2.50.
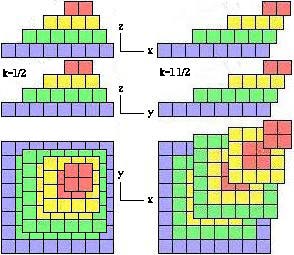
Figure 2.50. Glissements mutuels des strates selon la diagonale xy.
La description d'un tel glissement par le passage à un système de coordonnées obliques requiert maintenant deux angles obliques égaux, zx et zy. Les cases cubiques deviennent des prismes hexaédriques où sont préservés le volume, les faces carrées du haut et du bas et la hauteur, ayant quatre faces parallélogrammes dépourvues d'angle droit. Ces hexaèdres sont doublement penchés, l'angle devenant chaque fois phi au lieu de 90o, avec phi = arcctgk. L'identification des cases se fait sur la face supérieure des cases. Figure 2.51
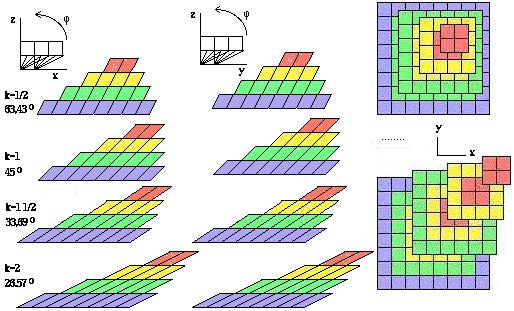
Figure 2.51. Coordonnées non trirectangles. R1O2. Glissements des strates. Profils, élévations, plans pour diverses valeurs de k. En plan, on montre la face supérieure des prismes.
Le système de coordonnées trirectangle R3 se trouve remplacé par un système R1O2 où deux des angles entre les axes sont obliques. La formule du système peut être celle qui suit.
R1(xy)O2[zx, zy, (phi, k)]
Le déplacement k est la somme vectorielle de deux déplacements égaux selon x et y. Ces derniers peuvent être + ou -, et ainsi, k peut être orienté selon chacun des quatre points intermédiaires principaux entre les points cardinaux. Convenons de briser les strates en quadrants et d'affecter chacun de ces quadrants du vecteur k centrifuge. Le résultat est remarquable : apparition de quatre pyramides à base carrée si k = 1/2, d'une étoile à quatre branches si k = 1 1/2. Figures 2.52.
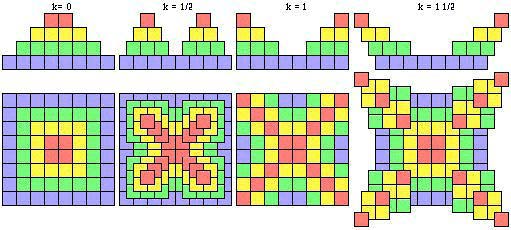
Figure 2.52. Systèmes R1O2 centrifuges pour chaque quadrant. Apparition de quatre pyramides à base carrée, d'une étoile à quatre branches.
Boules. Dans la figure précédente, remplaçons les cubes par des boules sphériques inscrites. Sur la base des 64 boules de la strate 4, les pyramides k = 1/2 tiennent parfaitement en équilibre à cause de la géométrie de la sphère, une boule s'appuyant sur trois. Avec un support adapté, l'étoile k = 1 1/2 tient en équilibre semblablement. La visibilité est excellente, car, en vue plongeante, seules quatre boules f de la strate 4 sont cachées.
Figures 2.53, 2.54.
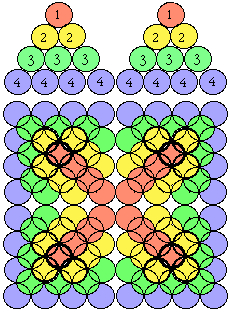
Figure 2.53. Quatre pyramides à base carrée. Boules au lieu de cubes.
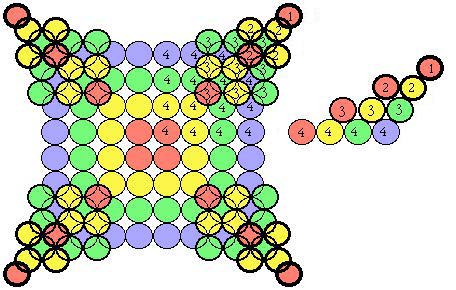
Figure 2.54. Étoile à quatre branches. Boules au lieu de cubes. Élévation d'une branche.
Jusqu'ici, l'introduction d'axes obliques selon zx et zy a respecté la forme carrée de la face supérieure et de la face inférieure du prisme hexaédrique. Notre nouvelle convention change cette forme en un losange en préservant la distance entre les côtés. Les angles zx et zy restent droits, de sorte que la formule du système nouveau peut s'écrire comme suit.
R2O1[xy(phi, k)]
Encore une fois, l'un des symboles phi ou k suffit. Les cases cubiques deviennent des prismes hexaédriques ayant deux faces losanges dépourvues d'angles droits et quatre faces rectangles égales.L'identification de la case prismatique se fait sur sa face supérieure. Nous allons nous contenter d'une valeur phi = 60o, k = 1 vaut la grande diagonale du losange. De la sorte, les faces losanges ont une petite diagonale égale à leur côté et dans ces losanges on peut reconnaître deux triangles équilatéraux assemblés.
Jetons et boules au lieu des losanges. Envisageons la strate 4. En remplaçant chaque prisme par un jeton cylindrique épais ayant même hauteur que le prisme et un diamètre convenable, nous obtenons, à cause de la géométrie du cercle, un assemblage régulier où chaque jeton en touche 2, 3 ou 6. Nous faisons de même pour les strates 3, 2, 1. La pyramide de la figure 2.45 devient un empilement stable de jetons. Figure 2.55.
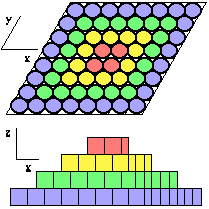
Figure 2.55. Système R2O1[xy(phi, k)]. Jetons. Vue en plan de la strate 4 et de l'empilement. Vue en élévation de l'empilement.
Envisageons encore la strate 4 en remplaçant les jetons par des boules de même diamètre.La projection verticale reste inchangée. Elle se divise en deux triangles équilatéraux égaux ayant une file de boules en commun ou, ce qui revient au même, en un grand triangle de 8 boules de côté et un petit triangle de 7 boules de côté. En faisant tourner le petit autour de la file commune, nous pouvons l'appliquer exactement sur le grand de façon que chacune de ses boules repose sur quatre. La strate occupe deux étages au lieu d'un. Figure 2.56.
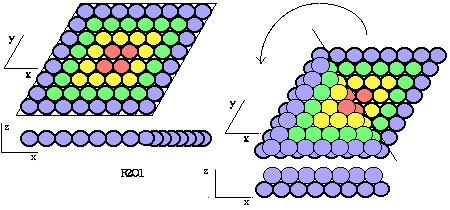
Figure 2.56. Système R2O1[xy(phi, k)]. Boules. Vue en plan de la strate 4. Rabattement et strate rabattue.
Après des opérations similaires sur les strates 3, 2, 1, nous obtenons finalement un empilement de quatre strates en 8 étages dessinant une pyramide à base triangulaire ou un tétraèdre. La pyramide de la figure 2.45 a doublé le nombre de ses étages et sa base est passée de carrée à triangulaire. Le nombre de cases au côté de sa base est resté le même.Figure 2.57.

Figure 2.57. Système R2O1[xy(phi, k)]. Boules Vue en plan de l'empilement de strates rabattues, vue de 2 faces et d'une seule. Nombres.
Ces deux nombres sont liés entre eux. Nous voyons qu'ils sont liés à la quantification de la configuration électronique du Québécium.
Précédent
Suivant
Introduction
Chapitre
1
Chapitre 3
Chapitre 4
Chapitre 5
Chapitre 6
Dernière mise
à jour
: 4 novembre
2000