2.3 Représentations bidimensionnelles

   Dans ce qui précède, la formule du Québécium se présente selon une seule dimension, avec toutefois des fragmentations et une exploitation des disponibilités de la feuille de papier ou de l'écran par des retours à la ligne et des mises en regard en colonnes, ce qui constitue une représentation bidimensionnelle non formalisée. De plus, plusieurs des groupements réalisés contiennent un nombre de termes indidivuels répondant au carré d'un nombre entier, ce qui suggère le recours à la géométrie du carré.Voyons maintenant comment les représentations bidimensionnelles peuvent nous servir : exploitation des mises en regard, géométrie des carrés. Voici d'abord quelques notions mathématiques utiles sur les matrices, les tableaux, les équerres et les couronnes.

2.3.1 Matrices

   Une matrice bidimensionnelle est un ensemble d'objets ordonné en lignes et en colonnes, emplissant un espace rectangulaire. Ainsi, une matrice 5X7 a 5 lignes, 7 colonnes et 35 objets. Chaque objet occupant une case carrée, une matrice occupe une grille, comme dans les mots croisés. Figure 2.1.


Figure 2.1. Matrice 5X7.

   Un alignement unidimensionnel d'objets comme celui du Tableau 2.2 est une matrice d'une ligne avec autant de colonnes qu'il y a d'objets, c'est une matrice ligne.Figure 2.2.


Figure 2.2. Matrice ligne 1X118.

   Une matrice carrée a un nombre égal de lignes et de colonnes. Figure2.3.


Figure 2.3. Matrice carrée 5X5.

   Une matrice ayant un nombre pair de lignes et de colonnes peut se décomposer en 4 matrices quadrants égales qu'on peut désigner par les points intermédiaires des points cardinaux NO, NE, SE, SO. Figure 2.4.


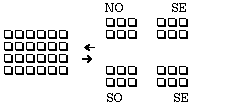
Figure 2.4. Décomposition d'une matrice paire-paire en 4 quadrants, composition d'une matrice paire-paire par 4 quadrants.

    Une matrice carrée possède une diagonale principale allant du coin NO au coin SE. Elle est dite symétrique si les cases symétriques par rapport à sa diagonale principale renferment des objets identiques. Figure 2.5.


Figure 2.5. Matrice symétrique 5X5.

   Dans une matrice diagonale unité, les cases de la diagonale principale renferment l'unité, les autres sont vides.Dans la matrice diagonale unité inverse, les cases de la diagonale NESO renferment l'unité, les autres cases sont vides. Figure 2.6.


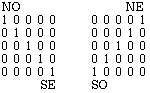
Figure 2.6. Matrice diagonale unité, matrice diagonale unité inverse.


   Les matrices se prêtent à des opérations de symétrie. Les résultats, que nous appellerons des retournements non superposables l'un à l'autre par des translations, sont au nombre de 8 dans le cas le plus général d'une matrice non symétrique. Quatre de ces retournements peuvent s'obteni par des rotations de pi/2 dans le plan, les autres requièrent en outre une opération de symétrie par rapport aux droites NS, OE, NOSE ou NESO. Dans le cas des matrices symétriques, on compte 4 retournements, qui peuvent tous s'obtenir par des rotations dans le plan. Figures 2.7, 2.8.


Figure 2.7. Les 8 retournements d'une matrice carrée, cas général.



Figure 2.8. Les 4 retournements d'une matrice carrée symétrique.

     Une opération habituelle dans la théorie des matrices peut nous servir, c'est la multiplication d'une matrice carrée multiplicande que nous supposons non symétrique afin d'examiner le cas général, par une matrice carrée diagonale unité inverse multiplicatrice. Cette opération fait passer la matrice multiplicande du retournement identité à un retournement qui n'est pas accessible par une rotation dans le plan. Voici comment se symbolise cette opération, qui équivaut à une opération symétrie par rapport à la droite NS. Figure2.9.


Figure 2.9. Multiplication d'une matrice par une matrice unité inverse. Notation algébrique avec indices affectant la lettre a, notation omettant la lettre a; notation libre pour la multiplication d'une autre matrice.

    La multiplication d'une matricecarrée multiplicande par une matrice carrée diagonale unité multiplicatrice donne la matrice multiplicande inchangée, elle équivaut à l'opérateur identité.

2.3.2 Tableau

   Un tableau est une portion de matrice dont les cases se touchent sans discontinuité. Un tableau peut toujours être remplacé par une matrice où on l'inscrit avec des cases vides. Toute matrice est un tableau. Figure 2.10


Figure 2.10. Tableau. Tableau inscrit dans une matrice 6X8.

   Un alignement unidimensionnel d'objets comme celui du Tableau 2.2 est aussi bien un tableau d'une ligne et 118 objets et ce tableau peut se remplacer par une matrice disons carrée de 118 lignes et 118 colonnes, 117 lignes restant vides. Figure 2.11.


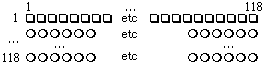
Figure 2.11. Matrice 118X118, 117 lignes vides.

   Ne pas confondre tableau matriciel comme ci-dessus et tableau rédactionnel.

2.3.3.1 Équerre

   Une équerre est un ensemble continu de cases dans un tableau, qui comporte une case centrale et deux bras autour d'elle : un bras comprend toutes les cases s'étendant horizontalement soit à droite soit à gauche jusqu'à la limite du tableau, et l'autre bras comprend toutes les cases s'étendant verticalement, soit vers le haut soit vers le bas jusqu'à la limite du tableau. Nous appellerons cases latérales les cases de ces bras. L'aspect est ainsi celui d'une équerre de menuisier. Une équerre peut exister isolément et constitue alors à elle seule un tableau. Une équerre peut se caractériser par la longueur de ses 2 bras, par exemple (2, -4) si un bras mesure 2 cases vers la droite et 4 cases vers le bas. Fig. 2.12.


Fig. 2.12. Équerre (2,-4) dans un tableau, équerre (2, -4) isolée.
   On peut attribuer une largeur et une hauteur à une équerre. Ainsi, pour l'équerre (2,-4), la largeur vaut 3 cases et la hauteur vaut 5 cases.

   Une équerre symétrique géométriquement peut s'appeler équerre carrée. Elle possède 2L cases latérales. Nous admettrons l'équerre symétrique avec L = 0, qui ne comporte qu'une case. Une équerre symétrique géométriquement renferme un nombre impair 2L+1 de cases, embrasse L2 cases et détermine une matrice carrée de (L+1)2 cases, ayant L+1 cases de côté. Figure 2.13.


Figure 2.13. Une équerre L = 4 renferme 9 cases, embrasse 16 cases et détermine une matrice carrée ayant 5 cases de côté et possédant 25 cases.
    Une telle équerre enferme L autres équerres symétriques, la plus petite ayant des bras nuls. Le total des cases de la matrice déterminée, pour L > 0, est (2L+1) .. +1.

   Ce total est la somme des nombres impairs consécutifs de 2L+1 à 1. On comprend ainsi mieux le nom de nombres carrés donné à la suite des nombres impairs, chacun correspondant à une équerre carrée. Toute matrice carrée renferme un nombre de cases carré d'entier, et elle se décompose en équerres dont le nombre de cases représente les nombres carrés jusqu'à 2L+1.

   Étant donné la notion de tableau, une équerre L = 1 peut se définir en peu de mots : ensemble continu de 3 cases non alignéesformant un tableau.


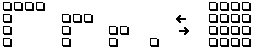
Figure 2.14. 4 équerres emboîtées, matrice 4X4, nombres impairs 1, 3, 5, 7.

   On peut composer et décomposer des matrices carrées en jouant sur l'emboîtage d'équerres de valeurs de L successives. Une matrice non carrée ne se décompose pas en équerres emboîtée régulièrement. Figure 2.14.

2.3.4.2 Couronne


   Quatre équerres isolées symétriques géométriquement ayant mêmes valeurs de L peuvent s'assembler pour former un ensemble continu de cases dans lesquelles on peut circuler dans un sens de rotation ou l'autre sans retour en arrière et en les touchant toutes, et revenir à la case dedépart.


Fig. 2.15. Couronne formée par 4 équerres L = 0. Couronne formée par 4 équerres L = 1.


   C'est ce que nous appellerons une couronne quadrangulaire. L'exemple le plus simple est celui de 4 équerres L= 0, donnant une couronne de 4 cases jointives. Avec L =1, la couronne enferme l'espace de 4 cases vides.

   Ces couronnes présentent un intéressant problème de combinatoire : possédant 4(2L+1) cases garnies chacune d'un objet différent, combien de configurations différentes obtient-on? La réponse est [4(2L+1)]! soit 4! = 24 et12! = 479 001 600 respectivement dans les exemples.

    Ce problème est un cas particulier d'un problème général de combinatoire imaginé et résolu par Pierre Auger dans une thèse de doctorat remarquable à l'UQAM en 1999.

2.3.4 Matrices carrées des demi-périodes

   Les carrés des entiers 1, 2, 3, 4, 6, 8 interviennent dans les représentations unidimensionnelles des demi-périodes et dans les strates. Cela suggère de produire des représentations bidimensionnelles de la configuration du Québécium dans des grilles carrées ayant 1, 2, 3, 4, 6, 8 cases de côté, capables de recevoir exactement les nombres voulus de termes des demi-périodes et des strates. Voici l'aspect de telles grilles constituées par des carrés d'imprimerie. Fig.2.16.


Figure 2.16. Aspect de grilles ayant 1, 2, 3, 4, 6 et 8 cases de côté.

   Le problème se pose alors de placer les termes dans les différentes cases. Il noussuffit d'envisager les demi-périodes et les grilles correspondantes ayant 1, 2, 3 ou 4 cases de côté, les autres grilles résultant de l'association de celles-ci. Une aide à cette fin provient de la notion d'équerre. Nous n'envisageons que des grilles carrées et des équerres symétriques.

   Puisque les demi-sous-couches ont 2l+1 soit 1, 3, 5 ou 7 termes, avec l = 0, 1, 2 ou 3, il est tout indiqué de les représenter sous l'aspect des équerres correspondantes ayant L = 0, 1, 2 ou 3. Les nombres quantiques l et les nombres L décrivant les équerres symétriques géométriquement co&itrem;ncident. Nous convenons de créer une grille carrée pour chaque demi-période et une équerre pour chaque demi-sous-couche représentéepar une ligne du Tableau 2.6. Parexemple, la demi-période 5, par des translations horizontales et verticales des termes individuels, donne deux équerres L = 1 et 0 et une grille de 2 cases de côté. La translation verticale est possible parce que nous faisons usage de bidimensionnalité. L'opération est particulièrement évidente lorsqu'on abrège l'écriture des termes individuels en ne conservant que les lettres symboles des valeurs du quantum azimutal. Fig. 2.17.


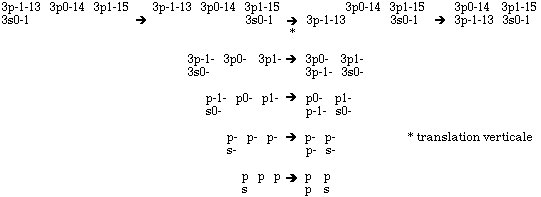
Figure 2.17. Passage d'une dimension à deux, création d'une équerre. Écriture complète des termes, écritures abrégées.
   ; L'opération de la figure 2.17 comporte une étape essentielle au passage de la représentation uni- à la représentation bi-dimensionnelle : c'est la translation verticale de certains termes d'une ligne. Associéeà des translations horizontales, elle équivaut à un rabattement à pi/2 ou au pliage d'une ligne de 3 termes p de manière à créer une équerre L = 1 qui emboîte le terme s équerre L = 0

   Si on recommence ces opérations sur les sous-périodescontenant des lignes d et f, des translations verticales sont nécessaires pour créer des équerresd et f à partir de ces lignes. L'agencement des lignes du Tableau 2.6 nous rend maintenant service.

   Des équerres carrées s'emboîtent de la sorte pour présenter chaque demi-période sous la forme d'une matrice. Dans une écriture abrégée, l'opération occupe un diagramme unique, conduisant à une matrice unique, réduite au besoin par suppression des cases f, des cases f et d ou des cases f, d et p, et aux retournements près. C'est une matrice type. Elle contient 16 cases. Figure 2.18.


Figure 2.18.Équerres emboîtables produisant une matrice type convenant à chaque demi-période. Une strate contient 4 telles matrices.

2.3.5 Strates et quadrants

   Les matrices types s'associent 4 par 4 pour former une strate (une matrice strate). Chacune est un quadrant se logeant dans l'un des angles droits déterminés par les axes NS et OE de la strate. Elles méritent bien le nom de quadrants. Une strate renferme 64 cases sous réserve de réductions.

2.3.6 Placements des quadrants et des termes

   Il nous faut décrire les retournements des quadrants et les placements des termes individuels dans les cases de chaque quadrant. Nous supposons que les termes individuels restent confinés à leurs équerres d'origine.

   Retournements.Ils sont ceux d'une matrice symétrique, pour autant que nous supposons l'équivalence, à l'intérieur d'une strate, entre tous les termes f, d, p et s, respectivement. Ils sont donc au nombre de 4 et ils diffèrent par un certain nombre de fois l'effet d'un verseur pi/2, en référence à la figure 2.8. Figure 2.19.


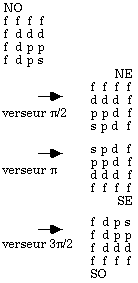
Fig. 2.19. Les 4 retournements des quadrants.

Précédent

Suivant

Introduction

Chapitre 1

Chapitre 2

Chapitre 3

Chapitre 4

Chapitre 5

Chapitre 6

Dernière mise à jour :4 novembre 2000