HetJa3d.htm
CECI EN VEILLEUSE16I2015Systme du
Qubcium.
Gomtrie et nombre magique 30. dification
d'un tableau symtrique 3D des lments, de l'Hydrogne 1 au Jantium 120.
par Pierre Demers
26 dcembre 2014.
Version du 3I2015.
Traduction interdite.
Un tableau 3D plutt que 2D.
Ceci continue un article dont le titre
contenait 2D au lieu de 3D. Rf. 1.
Un tableau 2D se prte aisment la
consultation parce qu'il est plong dans un monde 3D, qui laisse une dimension
libre pour y avoir accs. Un livre papier rclame d'tre feuillet, un
ordinateur, d'tre exploit. Un excellent exemple d'un tableau 3D est le
cerveau humain, que seul son porteur peut consulter. On connat le dicton :
"Quand un vieillard meurt, c'est une bibliothque qui s'croule".
Tant qu'on n'aura pas ralis une machine lire le contenu d'un tre humain,
veut veut pas! (Alors ce serait adieu aux mthodes de torture de la CIA.)
Une structure 3D clate d'objets opaques peut
certaines fois permettre au regard d'accder ce que l'auteur a voulu
installer et mettre en vidence. Cela implique un choix de ces objets parmi
d'autres. Les objets peuvent tre translucides. Par continut, on peut
imaginer un prolongement un lment de structure dont on n'aperoit qu'une
partie.
Ces mises en garde tant, voici en rappel deux
exemples de mes tableaux 3D. D'abord un chafaudage selon z de 4 surfaces
portant chacune l'criture de l'une des strates 2D, au lieu de les placer cte
cte dans un tableau en demi-ellipse. Les symboles eux-mmes des lments
restent 2D. L'espacement selon z peut se rgler pour qu'il n'y ait pas de
problme de lecture.
Un tableau
3D 4 tages plans.
Je transforme le tableau 2D en demi-ellipse en
un tableau 4 tages, une strate par tage. C'est une manire d'occuper 3D,
les strates conserevant leur statut 2D, tant crites disons sur un support
papier. Inspect de ct, il n'offre pas difficult particulire de lecture,
Ë venir.
Fig. 1. Le tableau en 4 tages, une strate
plane par tage
Ë venir.
Fig. 2.
Bimensionnalit
et tridimensionnalit: le passage, le rsultat.
2D: la chose placer tait 2D: une criture,
des chiffres. 3D: la chose placer 3D placer peut maintenant tre elle-mme
3D: un objet en ronde bosse. Je fais passer les cases de carrs plans des espaces
3D, des cellules occupes chacune par des sphres en assemblage compact. Je
remplace les cases 2D de Fig. 1 par des cubes.
Je pars du carrelage carr ayant 8 cases de
ct. Fig. 3. C'est Fig. 6 de Rf. 1, qui est 2D
Ouest - spin + Est
N
. .
.
S
Fig. 3. Carrelage carr ayant 8 cases de ct. Ouest O gauche, Est E droite. QbS2Fig297.3.gif
Copi de Rf. 1, Fig. 6.
Je remplace les carrs par des espaces cubiques
de mmes cts, destination quantifie RJVB. J'tablis un logement
cylindrique vide dans chaque espace cubique. La hauteur du cylindre gale son
diamtre. J'ai ainsi 64 espaces capables de recevoir les atomes de chaque
strate. Par glissement sans perdre contact entre les cylindres, je les fais
glisser vers l'Est, la range la plus au Sud tant garde fixe. Fig. 4.
J,attribue chaque espace un numro temporaire
de 1 64, en correspondance avec les cases du carrelage carr. Ainsi, je
destine les cases 29, 30, 36 et 37 des lments R, s.
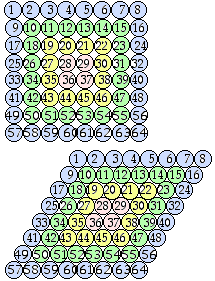
Fig. 4. Le carrelage de carrs est devenu un
carrelage de cylindres jointifs. On reconnat le trac de deux triangles
quilatraux 1, 64, 57 et 2, 8, 56.de mme diamtre. QbSyst2eFig018c
Je remplace les cylindres par des sphres de
mme diamtre. Dans une opration hors du plan de la figure, je ralise une
rotation sans perdre contact, rabattant la partie triangulaire d'un tenant 2,
8, 56 sur l'autre partie triangulaire 1, 64, 57 restant fixe. Fig. 5.
5. .
. .6
.6
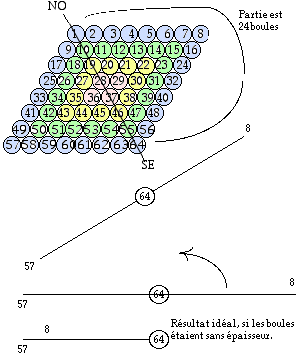
Figs 5, 6. Rabattement hors plan de la partie
2, 8, 56 sur la partie 1, 57, 64 qui reste fixe. Au cours de cette manoeuvre,
la boule 29 reste en contact avec les boules 28 et 37. Une fois la manoeuvre
termine, elle touche en plus la boule 36. QbSyst2eFig019c.gif QbSyst2eFig020c.gif,
Aprs le rabattement, le rsultat s'inscrit
dans un tronc de ttradre 2 niveaux. La sphre 29 repose sur les sphres 28,
36, 37, aussi bien que la sphre 56 repose sur les sphres 55, 63 et 64. Fig.
7.
. 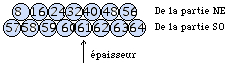 .
.
Fig. 7. Vue latrale de l'assemblage des 64
boules, il possde 2 niveaux suprieur 24 boules et infrieur 40 boules. Il
dessine un tronc de ttradre. QbSyst2eFig021.gif
Voici en numros temporaires.
Je signale une proprit d'un assemblage
compact de 4 sphres gales en contact 3D, chacune touchant les 3 autres: il
s'inscrit dans un ttradre rgulier, les centres des sphres dessinent un tel
ttradre. Vu sous un angle convenable, son image dessine un carr. Fig. 8.
.  .
.
Fig. 8. Assemblages de sphres dessinant 3D
un ttradre et 2D un carr. RetVbis2014-12-31
à 00.48.16.png
Je vois dans le carr dessin par les 4 boules
R la transposition du carr de 4 cases carrs renfermant les 4 lments H, He,
Li et Be de Fig. 9, avec cette diffrence qu'il y a 2 niveaux: 1H et 2He au
niveau suprieur et 3Li et 4B au niveau infrieur. Est est spin-, Ouest est
spin+,aussibienqu'en2D.
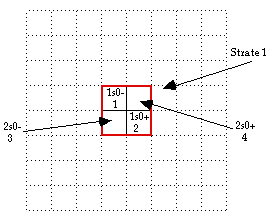
Fig. 9. Reproduite de Fig. 8 de Rf.1. Placement 2D de H et de He. QbS2Fig298
Dans
Fig. 8, les boules R suprieures reoivent 1H 1s0- au NO et 2He 1s0+ au
SE.
dification
du tableau ttradrique de 120 boules.
Rgle
1. Je me donne pour chaque
strate la structure portante dcrite ci-dessus, avec ses 64 cases pour boules
ddies RJVB, que je garnis partiellement sauf pour la 4e strate.
Rgle
2. Je reprsente une espce
atomique par une une boule selon le plandcritci-dessous..
Strate
1. Du dispositif de Fig. 5 que
voici nouveau, j'utilise les boules R exclusivement. La boule 29R vient se
loger au niveau suprieur, au dessus des boules 28R, 36R et 37R qui la
supportent. Le reste du dispositif Fig. 10 est inutilis.
Boules J. J20 vient se loger au-dessus de 19J, 27J et 28R; J21, au-dessus de J27, R28 et R36 R
Fig 5.
Les boules utilses sont 28, 37, 36; 29
Fig. 10. Ë venir.
Strate
2. J'utilise nouveau le dispositif
de Fig. 5. Boules R. Dans une 1re opration, je rpte mes actes dcrits pour
la strate 1 pour les boules R.
J'ajoute une opration sur les boules J.
Boules J. J20 vient se loger au-dessus
de 19J, 27J et 28R; J21, au-dessus de J27, R28 et R30; J22, au dessus de
J34, J 43 et J44 .
Rgle
d'ordonnance dans l'dification: E
Je commence en haut, gauche.
J'ai 12 boules J loger. Les boules s'associent naturellement en
ttrades.
De la sorte, la 1re ttrade gauche est de
signe -, la suivante est forme de 2 boules - puis 2 boules +.
|
La strate 2 rpte pour commencer la structure de la strate 1. S'ajoutent 3 ttrades
J. La 1re gauche est entirement -. La 2e a 2 boules- puis 2 boules +: elle
mixte - et +. La 3e ttrade est entirement+ |
|
La strate 3 rpte pour commencer la strate 2. S'ajoutent 5 ttrades V.
D'abord 2 entirement -. Puis une mixte - et +. Puis enfin 2 entirement +. |
|
La strate 4 rpte pour commencer la strate 3. S'aloutent 7 ttrades B. D'abord 3 entirement -.
Puis une mixte - et +. Puis enfin 3 entirement +. |
j21 audessus de
Conclusion.
Par les structures macroscopiques ainsi
ralises, j'espre mieux comprendre et faire comprendre les structures microscopiques des atomes eux-mmes.
Microscopiques et macroscopiques, ces structures ont des affinits de
symtries, il est plausible qu'elles aient des ressemblancesgomytques.
Pardonnez, si besoin est, mon usage frquent du
discours la 1re personne du singulier, que je crois ncessaire pour
distinguer les propositions que j'offre, de celles qui sont couramment admises.
J'invite le lecteur les rciter pour lui-mme.
Un atome est un objet compact, dont les parties
sont ramasses dans un trs petit espace. Sa reprsentation par des graphismes
2D ou 3D est trs loin de sa ralit; il faut y voir des bauches clates. Je
propose qu'un tel assemblage compact, mme s'il est difficile d'en inspecter
les parties, est plus prs de suggrer sa ralit.
Je passe du carrelage de carrs 2D un
empilement 3D compact ou clat, de boules. RJVB pour marquer le quantum SPDF,
le spin et Zeeman le quantum m sont discuts sparment.
Rfrences.